Simulating a random dynamical system
Power law properties of the dynamical systemDeveloping numerical simulations of a random dynamical system to depict intermittency and ergodicity breaking in some parameter regimes. Here is the code I developed for this project and the subsequent journal publication.
Description
We analysed the behaviour of a random map [1], which can be used to model random processes like Brownian motion.
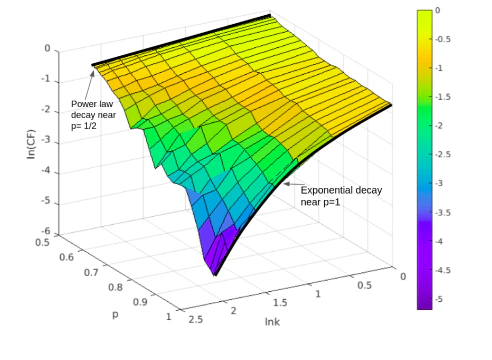
The probabilistic parameter p influences the behaviour of the map [2]. Due to the mod1 operation, we lose one bit of data at every iteration. Hence, we simulated the map using the MPFR package for arbitrary precision computation. We calculated the autocorrelation functions for the map at different parameter values and observed the decay in the function. We also computed other observables to capture ergodicity breaking, which occurs at certain p values.
Background
I worked on this project as a part of a summer research school organised by the London Mathematical Laboratory and the Abdus Salam International Center for Theoretical Physics. Dr. Yuzuru Sato, Dr. Rainer Klages and Dr. Stefano Ruffo were my supervisors.
I presented the preliminary results of this project as a talk at the end of the summer school, in July 2021.
References
[1] Pelikan, Stephan. “Invariant densities for random maps of the interval.” Transactions of the American Mathematical Society 281.2 (1984): 813-825.
[2] Sato, Yuzuru, and Rainer Klages. “Anomalous diffusion in random dynamical systems.” Physical review letters 122.17 (2019): 174101.
